News
With rapid advances in our experimental capability to perform quantum simulations, it is also important to ask what interesting physical phenomena we would like to explore. One interesting direction is the realization of deconfined quantum criticality (DQC), a concept central to the modern understanding of various quantum phase transitions yet experimentally unobserved phenomena.
In conventional settings, continuous phase transitions are often described by “order parameters”, i.e., local observables measuring spontaneous symmetry-breaking (SSB). According to the conventional framework of Landau-Ginzburg-Wilson theory, a continuous transition between two phases that spontaneously break distinct symmetries should be generically impossible since there is no a priori reason why the order parameter of one phase vanishes concomitantly as the order parameter of another develops. However, quantum mechanical effects can enable the said phenomena by intertwining order parameters for two distinct symmetries, where intertwined order parameters exhibit enlarged symmetry that was not present in the original model. This phenomenon is called deconfined quantum criticality (DQC).
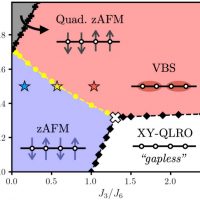
We have developed a way to probe DQC physics by using Rydberg quantum simulators. Figure 2 displays the rich phase diagram of the Rydberg atom array with exchange interactions arranged in a certain 1D geometry. Among many phases and phase transitions, we find that a particular phase transition, namely between zAFM and VBS phases, is continuous, yet cannot be explained by the conventional LGZ theory. It turns out, these phase transition points are described by a 1D version of deconfined quantum criticality. Our findings highlight Rydberg atom quantum simulators not only as promising platforms to experimentally realize such exotic phenomena, but also as unique ones allowing access to physical properties not obtainable in traditional experiments.
Figure: Phase diagram of Rydberg atom arrays with exchange interactions arranged in a zig-zag geometry. The phase transition along the yellow line cannot be explained by the conventional Landau-Ginzburg-Wilson (LGW) framework; it is an example of deconfined quantum criticality in 1D.