News
Reversing time for quantum-enhanced metrology
The group of Prof. Vuletic, at MIT, demonstrated that reversing the time in an atomic sensor can lead to a strongly enhanced sensitivity. With this time-reversal protocol, sensors can be operated with highly-entangled states which carry large statistical information close to the fundamental Heisenberg Limit. Due to their fragility, these “superior” quantum states are extremely hard to utilize in many (>20) atoms systems and, so far, have been mostly evanescent from the field of metrology. The robustness of the method demonstrated by Vuletic and colleagues opens to sensors operated near the fundamental Heisenberg limit.
State-of-the-art atomic sensors operate at the standard quantum limit (SQL), where the sensitivity of a sensor composed of atoms scales as
. However, the SQL is not a fundamental limit of many-atoms systems, if one allows establishing quantum correlations (entanglement) within the atoms. Quantum metrology aims at performances beyond the SQL, with its ultimate goal being the operation at the fundamental Heisenberg Limit. This limit requires the generation and detection of maximally entangled states, which are extremely fragile (losing a few atoms would destroy the whole state). Therefore, to date, only very simple and weakly entangled states that can not approach the Heisenberg Limit have been used.
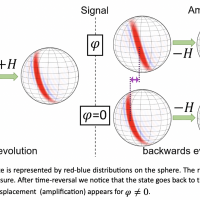
The MIT team demonstrated a time-reversal protocol, where a highly-entangled state is generated through a nonlinear evolution. Subjecting this state to a small signal and applying the nonlinear evolution backward (“time-reversal”) will generate a large amplification of the signal that can be easily read out (see Figure).
This result opens the field of time-reversal protocols and precision measurement with Heisenberg scaling near the Heisenberg limit, a regime that will be very important for future quantum sensors and fundamental precision measurements.
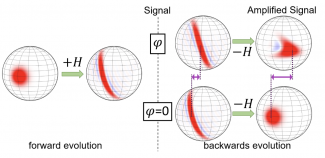
Figure : The collective state is represented by red-blue distributions on the sphere. The rotation angle phi (phase) is the signal we want to measure. After time-reversal we notice that the state goes back to the original one in the case of phi=0, while a large displacement (amplification) appears for phi does not equal 0 .